Fast decompression for
web-based
view-dependent
3D rendering

Federico Ponchio and Matteo Dellepiane
VCG - ISTI - CNR

Goal

Efficient transmission and rendering
of (large) 3D meshes (on the web)

(we are not concerned with the user interface here)

• Progressive: quality of the rendering improves as data is downloaded incrementally
• Adaptive: resolution of the triangles changes dynamically across the model depending on the view-point
• Maximize throughput: triangles per second sent from server to GPU

Batched multitriangulation

The mesh is decomposed into small patches of thousands of triangles at different resolution.

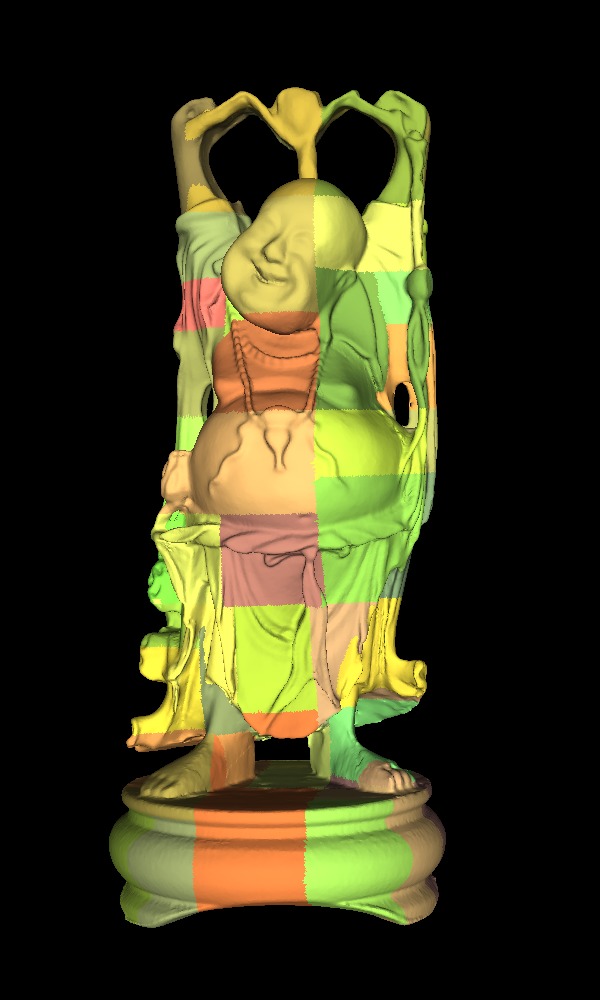
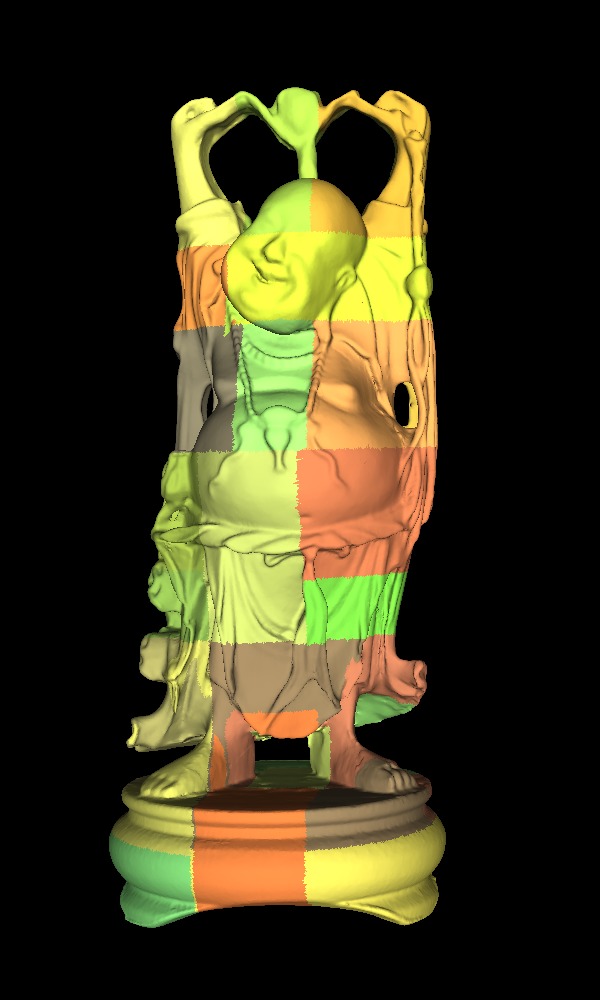
And assembled back at variable resolution:

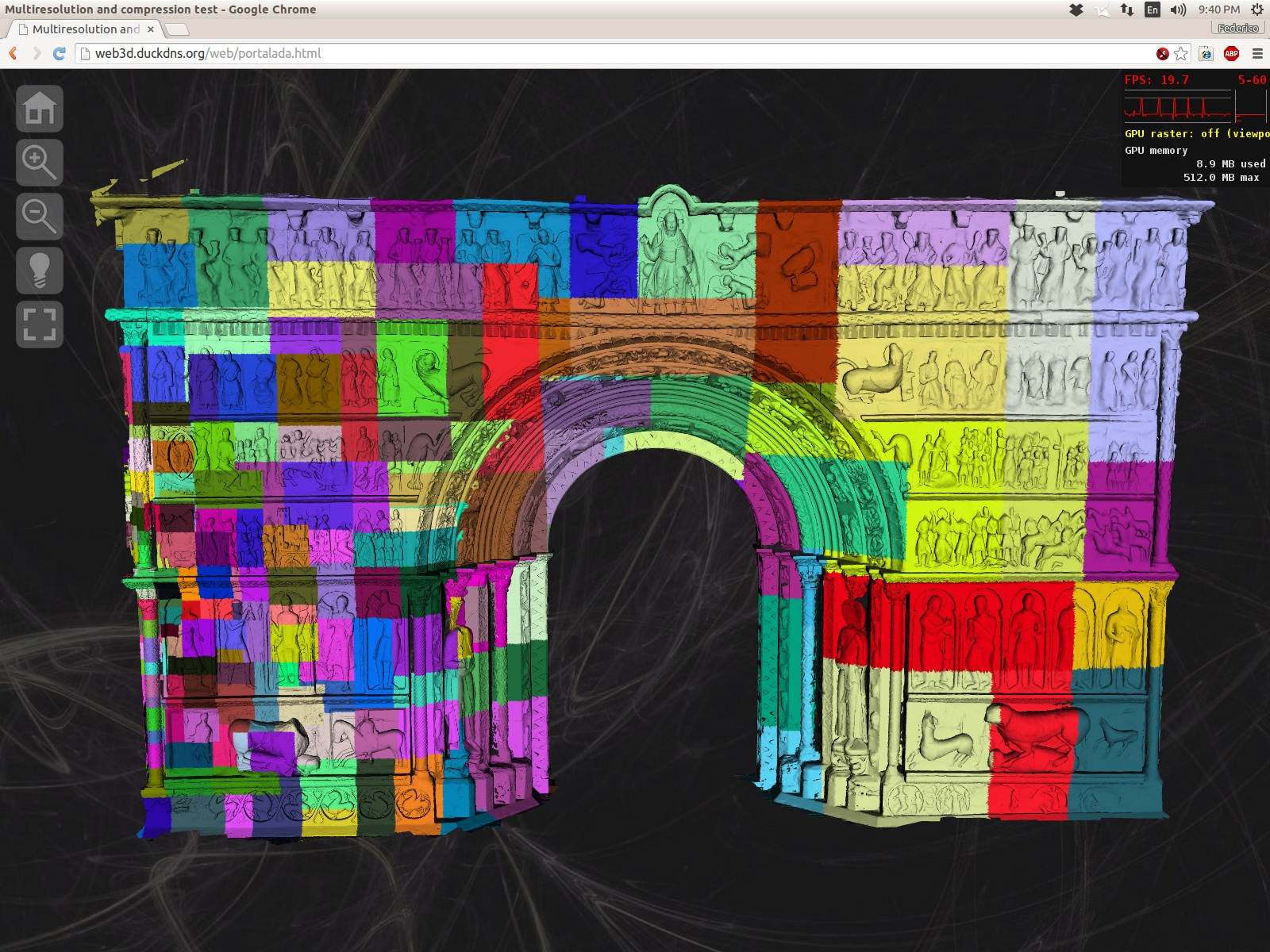
so that the resolution on screen is approximately constant.

Of course it is a bit more complicated than this.

You can find the gory details on my PhD thesis:

http://vcg.isti.cnr.it/~ponchio/download/ponchio_phd.pdf

Advantages

• Low CPU: a simple traversal of a small tree is required
• Trivially out-of-core: each patch is just a mesh.
• Shader agnostic and GPU friendly this is just geometry.

That's perfect for the web...but also for native implementations.

Disadvantages

• Doubles size (!)
• Reduced granularity
• Duplicated patch borders

Data layout:

struct IndexEntry {
  unsigned short n_of_vertices; //64k vertex max.
  unsigned short n_of_triangles; 
  int patch offset;              
  float error;
  vec4f bounding_sphere; 
}; //32 Bytes

Loading data

• HTTP range requests random access and no server overhead
• Small index loaded first actually we just need the beginning of the index to start
• Pipelining no slower than downloading the whole file at once
• Periodic caching bugs in browsers sometimes we have to disable caching until the bug is sorted out :(

Rendering

• Tree traversal taking into account available patches triangle budget view-dependent error
• Bind buffers and glDrawElements call for each patch
• Prefetching
• Adjust triangle budget for optimal FPS (optional)

Mesh compression

Any mesh compression algorithm can be used
if we compress each patch separately
(es. OpenCTM, WebGL-Loader, PopBuffers).

As long as

• allows random access to patches
• ensure consistency of patch borders

Of course we developed a new one.

Choices, choices, choices

• Topological compression
• Parallelogram prediction
• Global quantization
• Tunstall for entropy compression

Compression ratio vs. decompression speed

The best spot depends on the available bandwidth
and processing power.

From: Limpey et al. Fast Delivery of 3D Web Content: A Case Study

Topological compression

Modified version of edgebreaker:
turns a mesh into a sequence of symbols.

Boundary

We keep a linked list of the boundary, and a list of unprocessed edges.

Operations

Split

• Happens when the boundary meets itself
• we just encode the index of the vertex
• the boundary is NOT splitted into 2 rings this would require reconstructing topology
• since the ring is never split the decoded mesh is a disk

Glue

• happens because we do not actually split
• these s symbols could be spared if we did split, but keeping track of topology is expensive

In practice, these expensive operations can be minimized processing active edges in an appropriate order.

Global quantization

The error value in the patches is used to automatically pick quantization steps.

This ensures consistency across borders.

Parallelogram prediction

New vertex positions are estimated, and the differences from the actual position encoded.

This is especially effective for regular meshes.

Encoding differences

The first stream will be compressed

The dictionary becomes very small (and thus fast).

We assume that nearby difference values have similar probability.

Entropy compression

We can approximate our streams as a pure entropic source with no memory and fixed frequencies.

• Dictionary based, adaptive (LZMA, LZW, etc) dictionary updates are costly
• Arithmetic encoding bit maniputlation intensive
• Huffman with table lookup (Pajarola), table creation is expensive
• Tunstall variable length to fixed size word, again table lookup

Tunstall

Variable number of symbols to a fixed size word (es. a byte)

In decompression each byte is decompressed to a variable number of symbols

Entropy decompression speed

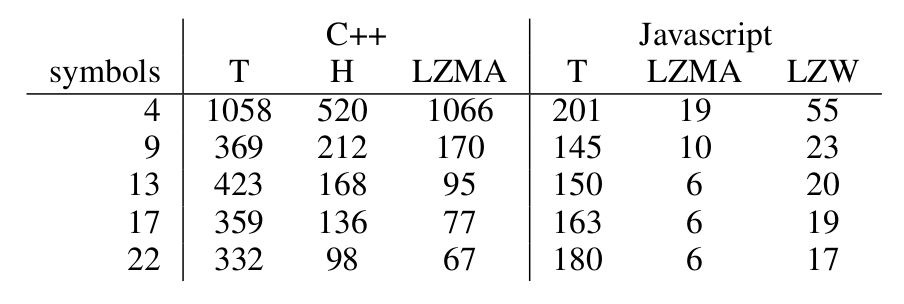
32.000 symbols, poisson distribution, iCore5 3.1Gh

Tunstall has about 10% worse compression.

Mesh decompression speed

1-3 million triangle per second in Javascript single thread, Chrome, difficult to measure exactly

16 million triangles per second in C++

This includes normals and color per vertex

Source code and executables?

Nexus library: available at http://vcg.isti.cnr.it/nexus

3dHop (includes windows executables and interface): http://vcg.isti.cnr.it/3dhop

Versions with compression support to be released shortly.

Demo?

http://web3d.duckdns.org

Normals

Estimating them using faces and vertices is quite fast.

We can then encode the differences, rememebr we need borders to match.

Colors

We change colorspace for better coherence

Quantize and encode differences as usual

Point clouds

Implemented (but not in the paper...)

Interleave the bits, sort by z-order, encode difference as number of different bit and the differetn bits as usual

Textures

Not implemented yet (wait next year)

The format support projective textures and texture coordinates

WebGL-Loader

We plan to add support for this algorithm, especially for mobile

Javascript optimization

Allocation of arraybuffer is costly.

using ArrayBuffer directly is fast(er than copying variables around)

Manually inlining functions? Yes, legibility suffer but gains are substantial

Integer aritmetic is possible but painful. Very painful.
Use a C++ reference implementation.

Themes